Авинаш диксит: теория игр. искусство стратегического мышления в бизнесе и жизни

Обратные рассуждения

Метод обратных рассуждений заключается в том, что вы заглядываете в будущее и продумываете шаги к победе в обратном порядке. Начнем с простой ситуации:

В книге авторы описывают случай, который произошел с их знакомым. Знакомый, назовем его Николай, собирался на концерт на открытом воздухе. Конечно, Николай хотел расположиться поближе к сцене и пришел пораньше, чтобы выбрать место. Накануне прошел дождь, у сцены земля превратилась в грязь. Поэтому Николай отошел туда, где грязь заканчивалась, постелил одеяло, достал бутерброды и стал ждать зрелища.

Проблема в том, что никто из зрителей не хотел садиться в грязь, поэтому скоро все чистые участки закончились, а потом зрители стали заполнять участок рядом со сценой, но из-за грязи они не садились, а стояли. В конце концов Николай сидел на земле и ничего не видел за стоящими зрителями, которые вдобавок истоптали ему одеяло.

Метод обратных рассуждений спас бы Николая от этой ситуации. Если бы он мыслил стратегически, он бы представил, что будет, когда соберутся зрители. То есть действовал из будущего к настоящему. И принимал бы решение, исходя их будущего.

Этот метод работает в играх, где соперники ходят по очереди, а количество ходов ограничено. Например, на поле установлен 21 флажок. Вы с соперником по очереди вытаскиваете 1, 2 или 3 флажка за ход. Тот, кто возьмет последний флажок, побеждает. Ход верных рассуждений: чтобы победить, в конце игры я оставлю соперника с четырьмя флажками, сколько бы он не вытащил, я заберу остальные и выиграю. Чтобы оставить соперника с четырьмя флажками на последнем ходу, я должен оставить его с восьмью на предпоследнем. И так вы прокручиваете ходы до начала игры.

То же самое стратегически мыслящие люди делают в работе и бизнесе:

Допустим, партнер предлагает инвестировать в разработку нового продукта 1 000 000 ₽. Он обещает, что через год этот миллион превратится в 5 000 000 ₽, и вы поделите прибыль пополам. Партнер при этом ничего не вкладывает, но берет на себя заботы по производству. Есть риск того, что расчеты партнера неверны, поэтому вы не знаете, стоит ли принимать предложение. Для наглядности авторы книги предлагают рисовать схему:

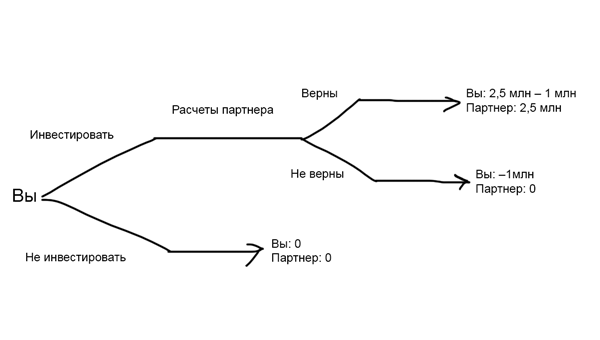
Схема помогает увидеть математическую вероятность и цену проигрыша. После этого вы оцениваете более субъективные данные, в которых математика не поможет: насколько вы доверяете партнеру, нравится ли идея, есть ли деньги на реализацию. Когда собрали всю информацию, принимаете решение. В ситуации нет победителя и проигравшего. Вы оба либо выигрываете, либо проигрываете, и никому не выгоден проигрыш.

Это простой пример. Чаще бывает больше вариантов или больше участников. Тогда схемы получаются более разветвленные и наглядные. Польза в том, что вы не держите в голове все условия, которые влияют на решение. Рисуете их на бумаге и видите факты, которые создают ясность. Такие схемы помогают спланировать поездку, купить квартиру, выбрать место работы.

Проклятие победителя

Проклятие победителя — разочарование, которое испытывают люди после покупки дорогой вещи. Чаще всего это чувство связано с победой на аукционах или с покупкой акций на фондовой бирже. Хотя то же самое случается с обычными покупками, работой с клиентом, личной жизнью:

Вы узнаете о выходе новых умных часов. Делаете предзаказ, ждете два месяца, получаете и разочаровываетесь. Половина функций вам не нужна, выглядят не так, как на картинке, а пользоваться неудобно.

Мужчина делает девушке предложение. Они женятся, а в реальности все не так романтично, как казалось до брака.

Компания полгода охотится за крупным клиентом и наконец договаривается о встрече. Клиент принимает коммерческое предложение, вы беретесь за работу, а он оказывается слишком капризным. В итоге ресурсов на него уходит больше, чем рассчитывали, а результат не оправдывает ожидания.

«.=»» Киса=»» и=»» Остап»=»»>
Проклятие победителя преследовало Остапа и Кису

Мы называем это ошибкой или разочарованием, а теория игр «проклятием победителя» и подходит к проблеме стратегически. Проклятие победителя возникает по трем причинам:

нехватка информации. Из-за того, что мы слишком мало знаем о предмете, мы его переоцениваем и получаем завышенные ожидания. В примере с клиентом компания видела только потенциальную прибыль, но не изучила стиль управления у компании-клиента и все то, что повлияет на работу. Очевидное решение — собирать как можно больше информации перед принятием решения;

завышенная личная ценность. Каждая вещь обладает двумя видами ценности: личной и общей. Сувенир из детского путешествия с родителями лично для вас будет ценным, потому что связан с воспоминаниями. Для остальных это просто безделушка без общей ценности. И наоборот, антиквариат на аукционе имеет высокую общую ценность, но это не значит, что он будет ценным именно для вас. В примере с часами сработал этот принцип: рекламщики создали ажиотаж вокруг гаджета, что повысило его общую ценность в глазах потребителей. Покупатель ориентировался на общую ценность, но не учел личной, поэтому разочаровался.

Чтобы не разочаровываться, сначала изучите предмет, определите для него личную ценность в денежном эквиваленте и только потом выясняйте рыночную стоимость. Если она выше той, которую вы сами определили, откажитесь от покупки. Если такая же или ниже — покупайте. Такой подход помогает не разочароваться, хотя и кажется занудным;

соревновательность. Это характерно для покупок на аукционах или дефицитных товаров. Покупатель входит в азарт и готов отдать любые деньги, чтобы быть единственным или одним из немногих обладателей вещи. Если хотите поддаться азарту и выиграть — анализируйте личную ценность вещи для остальных участников торга и предлагайте большую цену. А если не хотите потом разочароваться — снова определите личную ценность и не поддавайтесь соблазну всех победить.

Общий совет, который дают авторы книги «Теория игр» — играть так, будто вы уже выиграли: сначала оцениваете последствия, а потом принимаете решение о покупке и деньгах, которые готовы заплатить.

Игра в орлянку

В орлянке участвуют Игрок 1 и Игрок 2. Каждый игрок одновременно выбирает орла или решку. Если они угадывают, Игрок 1 получает пенс Игрока 2. Если же нет — Игрок 2 получает монету Игрока 1.

Выигрышная матрица проста…

…оптимальная стратегия: играйте полностью наугад. Это сложнее, чем вы думаете, потому что выбор должен быть абсолютно случайным. Если у вас есть предпочтения орла или решки, противник может использовать его, чтобы забрать ваши деньги.

Конечно, настоящая проблема здесь заключается в том, что было бы намного лучше, если бы они просто бросали один пенс друг в друга. В результате их прибыль была бы такой же, а полученная травма могла бы помочь этим несчастным людям почувствовать что-то, кроме ужасной скуки. Ведь это худшая игра из существующих когда-либо. И это идеальная модель для серии пенальти.

Практическое применение: Пенальти

В футболе, хоккее и многих других играх, дополнительное время — это серия пенальти. И они были бы интереснее, если бы строились на том, сколько раз игроки в полной форме смогут сделать «колесо», потому что это, по крайней мере, было бы показателем их физических способностей и на это было бы забавно посмотреть. Вратари не могут чётко определить движение мяча или шайбы в самом начале их движения, потому что, к огромному сожалению, в наших спортивных состязаниях роботы все еще не участвуют. Вратарь должен выбрать левое или правое направление и надеяться, что его выбор совпадет с выбором противника, бьющего по воротам. В этом есть что-то общее с игрой в монетку.

Однако обратите внимание, что это не идеальный пример сходства с игрой в орла и решку, потому что даже при правильном выборе направления вратарь может не поймать мяч, а нападающий может не попасть по воротам. Итак, каково же наше заключение согласно теории игр? Игры с мячом должны заканчиваться способом «мультимяча», где каждую минуту игрокам один на один выводится дополнительный мяч/шайба, до получения одной из сторон определенного результата, который был показателем настоящего мастерства игроков, а не эффектным случайным совпадением

Итак, каково же наше заключение согласно теории игр? Игры с мячом должны заканчиваться способом «мультимяча», где каждую минуту игрокам один на один выводится дополнительный мяч/шайба, до получения одной из сторон определенного результата, который был показателем настоящего мастерства игроков, а не эффектным случайным совпадением.

В конце концов, теория игр должна использоваться для того, чтобы сделать игру умнее. А значит лучше.

• Посмотрите, как взрывается ваша еда
• Вот почему нельзя кипятить воду дважды!
• Воображаемые счёты: сложные вычисления «на пальцах»
• Фастфуд наносит организму больше вреда, если запивать его кофе
• 10 фактов о том, почему мы испытываем дежавю

Применение теории игр

Если говорить о математической теории игр, то в настоящее время она находится на стадии активного развития. Но математическая база по своей сути является очень затратной, по причине чего применяется она, главным образом, только если цели оправдывают средства, а именно: в политике, экономике монополий и распределения рыночной власти и т.д. В остальном же, теория игр применяется в исследованиях поведения людей и животных в огромном количестве ситуаций.

Как уже и было сказано, сначала теория игр развивалась в пределах границ экономической науки, благодаря чему стало возможным определить и интерпретировать поведение в различных ситуациях экономических агентов. Но позже область её применения значительно расширилась и стала включать в себя множество социальных наук, благодаря чему с помощью теории игр сегодня объясняется поведение человека в психологии, социологии и политологии.

Специалисты используют теорию игр не только для того чтобы объяснить и предсказать человеческое поведение – было предпринято множество попыток по использованию этой теории с целью разработать эталонное поведение. Кроме того, философы и экономисты долгое время при помощи неё старались как можно лучше понять хорошее или достойное поведение.

Таким образом, можно заключить, что теория игр стала настоящим переломным моментом в развитии множества наук, и сегодня является неотъемлемой частью процесса изучения различных аспектов поведения человека.

ВМЕСТО ЗАКЛЮЧЕНИЯ: Как вы заметили, теория игр довольно тесно взаимосвязана с конфликтологией – наукой, посвящённой изучению поведения людей в процессе конфликтного взаимодействия. И, на наш взгляд, эта область является одной из самых главных не только среди тех, в которых теория игр должна применяться, но и среди тех, которые должен изучать сам человек, ведь конфликты, как ни крути, являются частью нашей жизни.

Если у вас есть желание разобраться в том, каким образом лучше всего вести себя в конфликтах, и какие вообще существуют стратегии поведения в них, мы предлагаем вам пройти наш курс по самопознанию, который в полной мере предоставит вам такую информацию. Но, помимо этого, пройдя наш курс, вы сможете провести всестороннюю оценку своей личности вообще. А это значит, что вы будете знать и о том, как вести себя в случае конфликта, и каковы ваши личностные преимущества и недостатки, жизненные ценности и приоритеты, предрасположенности к работе и творчеству, и много чего ещё. В общем, это очень полезный и нужный инструмент для каждого, кто стремится к развитию.

Наш курс находится здесь – смело приступайте к самопознанию и совершенствуйте себя.

Мы желаем вам успехов и умения быть победителем в любой игре!

История теории игр

Наиболее оптимальные стратегии в области математического моделирования учёные предлагали ещё в XVIII веке. В XIX веке задачи ценообразования и производства в условиях рынка с малой конкуренцией, впоследствии ставшие классическими примерами теории игр, рассматривались такими учёными, как Жозеф Бертран и Антуан Курно. А в начале XX столетия выдающимися математиками Эмилем Борелем и Эрнстом Цермело была выдвинута идея математической теории конфликта интересов.

Истоки математической теории игр следует искать в неоклассической экономике. Изначально основы и аспекты этой теории излагались в работе Оскара Моргенштерна и Джона фон Неймана «Теория игр и экономическое поведение» в 1944 году.

Представленная математическая область также нашла некоторое отражение и в социальной культуре. Например, в 1998 году Сильвия Назар (американская журналистка и писательница) выпустила книгу, посвящённую Джону Нэшу – лауреату Нобелевской премии по экономике и специалисту по теории игр. В 2001 году по мотивам данной работы сняли фильм «Игры разума». А ряд американских телешоу, таких как «NUMB3RS», «Alias» и «Friend or Foe» время от времени в своих эфирах также ссылаются на теорию игр.

Но отдельно следует сказать о Джоне Нэше.

В 1949 году им была написана диссертация на тему теории игр, а через 45 лет он был удостоен Нобелевской премии по экономике. В самых первых концепциях теории игр подвергались анализу игры антагонистического типа, в которых имеются игроки, выигравшие за счёт проигравших. Но Джон Нэш разработал такие аналитические методы, согласно которым все игроки либо проигрывают, либо выигрывают.

Разработанные Нэшем ситуации впоследствии назвали «равновесием по Нэшу». Отличаются они тем, что все стороны игры применяют наиболее оптимальные стратегии, благодаря чему и создаётся устойчивое равновесие. Сохранять равновесие очень выгодно для игроков, ведь в противном случае какое-то одно изменение может негативно сказаться на их положении.

Благодаря деятельности Джона Нэша теория игр получила мощный толчок в своём развитии. Кроме того, были подвергнуты серьёзному пересмотру математические инструменты экономического моделирования. Джон Нэш смог доказать, что классическая точка зрения на вопрос конкуренции, где каждый играет только за себя, не является оптимальной, и самыми эффективными стратегиями являются такие, в которых игроки делают лучше себе, изначально делая лучше другим.

Несмотря на то, что изначально в поле зрения теории игр находились и экономические модели, до 50-х годов прошлого века она была лишь формальной теорией, ограниченной рамками математики. Однако со второй половины XX века предпринимаются попытки её использования и в экономике, и в антропологии, и в технике, и в кибернетике, и в биологии. В период Второй мировой войны и по её окончании теорию игр начали рассматривать военные, разглядевшие в ней серьёзный аппарат в деле развития стратегических решений.

В период 60-70-х годов интерес к данной теории угас, невзирая даже на то, что она давала хорошие математические результаты. Но с 80-х годов начинается активное применение теории игр на практике, главным образом, в менеджменте и экономике. В течение же нескольких последних десятилетий актуальность её значительно выросла, а некоторые современные экономические направления и вовсе невозможно представить без неё.

Не будет лишним сказать также и о том, что существенный вклад в развитие теории игр внёс труд «Стратегия конфликта» 2005 года лауреата Нобелевской премии по экономике Томаса Шеллинга. В своей работе Шеллинг рассмотрел множество стратегий, которыми пользуются участники конфликтного взаимодействия. Данные стратегии совпали с тактиками конфликт-менеджмента и аналитическими принципами, применяющимися в конфликтологии, а также с тактиками, которые используются для управления конфликтами в организациях.

В психологической науке и ряде других дисциплин понятие «игра» имеет несколько иной смысл, чем в математике. Культурологическая интерпретация термина «игра» была представлена в книге «Homo Ludens» Йохана Хёйзинга, где автор толкует о применении игр в этике, культуре и правосудии, а также указывает на то, что сама игра существенно превосходит человека по возрасту, ведь и животные тоже склонны играть.

Также понятие «игра» можно встретить в концепции Эрика Бёрна, известного по книге «Люди, которые играют в игры». Здесь, правда, идёт речь об исключительно психологических играх, основой которых является трансакционный анализ.

Общие советы

Теория игр сложнее и интереснее, чем я описала. Если вам хорошо дается математика, изучите ее тщательнее, так она принесет вам гораздо больше пользы. А если математика вас не очень интересует, воспользуйтесь этими общими советами в ситуациях, когда приходится делать выбор:

не торопитесь с ответом. Дайте себе время подумать прежде чем принимать решение. Изучите вопрос как следует, соберите максимум информации и проанализируйте выгоду и убыток от каждого из вариантов. Не всегда оптимальным решением будет то, которое принесет больше денег. Иногда оно более рискованное, поэтому оценивайте не только выгоду, но и риски;

ставьте себя на место соперника. Проанализируйте его мотивы и возможные действия. Скорее всего, вы учитываете не все обстоятельства. Авторы рассказывают о случае, когда таксист завысил цену на поездку, а они предложили ему меньше денег в надежде поторговаться. Таксист разозлился, отвез их обратно к пункту отправления и высадил из машины. Обстоятельства, которые авторы могли не учесть: у таксиста был тяжелый день; на переднем сидении сидела его невеста, и он из гордости не собирался уступать; счетчик в машине сломался, поэтому он предложил фиксированную стоимость поездки. Стратегическое мышление включает умение вставать на место другого игрока и просчитывать его ходы. Возможно, соперник тоже знает теорию игр;

будьте готовы проиграть. Хотя в блоке о проклятии победителя авторы советуют играть так, будто вы уже выиграли, это не значит, что надо слишком рассчитывать на победу. В этом случае появляется нужда, а нужда — путь к провалу. Об этом мы уже писали

Поэтому анализируйте решение так, будто выиграли, но будьте готовы к поражению, чтобы не завышать важность победы

Статья Людмилы Сарычевой

Равновесие Нэша

Равновесие Нэша — это набор ходов, где никто не хочет сделать что-то по-другому после свершившегося факта. И если мы сможем заставить это работать, теория игр заменит всю философскую, религиозную, и финансовую систему на планете, потому что «желание не прогореть» стало для человечества более мощной движущей силой, чем огонь.

Давайте быстро поделим 100$. Вы и я решаем, сколько из сотни мы требуем и одновременно озвучиваем суммы. Если наша общая сумма меньше ста, каждый получает то, что хотел. Если общее количество больше ста, тот, кто попросил наименьшее количество, получает желаемую сумму, а более жадный человек получает то, что осталось. Если мы просим одинаковую сумму, каждый получает 50 $. Сколько вы попросите? Как вы разделите деньги? Существует единственный выигрышный ход.

Требование 51 $ даст вам максимальную сумму независимо от того, что выберет ваш противник. Если он попросит больше, вы получите 51 $. Если он попросит 50 $ или 51 $, вы получите 50 $. И если он попросит меньше 50 $, вы получите 51 $. В любом случае нет никакого другого варианта, который принесет вам больше денег, чем этот. Равновесие Нэша — ситуация, в которой мы оба выбираем 51 $.

Практическое применение: сначала думайте

В этом вся суть теории игр. Не обязательно выиграть и тем более навредить другим игрокам, но обязательно сделать лучший для себя ход, независимо от того, что подготовят для вас окружающие. И даже лучше, если этот ход будет выгоден и для других игроков. Это своего рода математика, которая могла бы изменить общество.

Интересный вариант этой идеи — распитие спиртного, которое можно назвать Равновесием Нэша с временной зависимостью. Когда вы достаточно много пьете, то не заботитесь о поступках других людей независимо от того, что они делают, но на следующий день вы очень жалеете, что не поступили иначе.

Случайный выбор

Собеседник предлагает игру: в одной руке у него монета, в другой — ничего. Угадаете где монета, заберете себе. Не угадаете — достанется сопернику. В этой игре победитель получает выигрыш за счет проигравшего. Не получится так, что все будут довольны или огорчены.

Представьте ход мыслей, если воспользуетесь методом обратных рассуждений:

Соперник знает, что я правша и, скорее всего, выберу правую руку, поэтому он вложил монетку в левую. Но еще он знает, что я не дурак и знаю, что он так и сделает, поэтому наверняка он все равно вложил в правую. Но он может знать, что я знаю, что он знает…

Так же может рассуждать соперник, когда будет прятать монетку. В любом случае такое рассуждение заведет в тупик. Поэтому здесь полезнее использовать метод случайного выбора.

Этот подход не выглядит стратегическим, но в подобных ситуациях он самый стратегически продуманный из всех возможных.

Авторы приводят аналогию с игрой «Камень, ножницы, бумага». Если вы будете выбрасывать варианты в конкретном порядке, соперник попытается его разгадать. Возможно, у него это получится. Если вы используете метод случайного выбора, шансы на победу возрастают, потому что вы сами не знаете свой следующий выбор. А соперник и подавно.

То же самое с орлом и решкой. Если первый раз выпал орел, то вероятность, что он выпадет во второй — пятьдесят на пятьдесят. Обычно люди об это забывают и в следующий раз ставят на противоположный вариант.

Этот подход работает и в спорте. Например, игрок выбивает пенальти. Вратарь знает, что игрок обычно бьет с правой ноги и подстраивается под это. С другой стороны, он понимает, что игрок тоже предусматривает рассуждение вратаря и может подать мяч левой ногой. Поэтому лучше не продумывать, а подать любой удобной ногой и вообще все время бить пенальти по-разному, чтобы никто не мог предсказать ваши действия. Хотя, конечно, точность удара пострадает, в целом шансы на победу растут за счет непредсказуемости.

«»=»»>
В фильме «Человек, который изменил все» герой Бреда Питта вместе с помощником-экономистом набирает игроков по статистике ударов. Эти игроки считаются бесперспективными, но благодаря математике и непредсказуемому подходу, команда выигрывает двадцать игр подряд

В бизнесе редко встречаются ситуации, где подходит метод случайного выбора. Обычно лучше работает анализ и переговоры с конкурентами.

Кока-Кола и Пепсико — крупные конкурирующие компании. В ситуации, когда они выставляют одинаковые цены, у каждой свои покупатели. Но если кто-то из них предлагает скидки, часть покупателей переходит к этой компании.

Конечно, Кока-Коле невыгодно, когда Пепсико запускает скидочную кампанию. Поэтому она готовит ответную кампанию, запускает после Пепсико и переманивает потребителей.

Так продолжается, пока они случайно не запускают кампании одновременно. Если это происходит, то потребители не переходят от одной компании к другой, а просто получают скидки. Обе компании несут убытки: продали продукцию дешевле, а новых потребителей не привлекли. Потребителю выгодно переходить от одной компании к другой, только когда есть разницы в цене. В этом случае ее нет. Понимая, что это во взаимных интересах, Пепсико и Кока-Кола договорились проводить акции по очереди.

Используйте метод случайно выбора там, где противник пытается предугадать ваши действия.

Дилемма заключенного

Берто и Роберт были арестованы за ограбление банка, не сумев правильно использовать для побега угнанный автомобиль. Полиция не может доказать, что именно они ограбили банк, но поймала их с поличным в украденном автомобиле. Их развели по разным комнатам и каждому предложили сделку: сдать сообщника и отправить его за решетку на 10 лет, а самому выйти на свободу. Но если они оба сдадут друг друга, то каждый получит по 7 лет. Если же никто ничего не скажет, то оба сядут на 2 года только за угон автомобиля.

Получается, что, если Берто молчит, но Роберт сдает его, Берто садится в тюрьму на 10 лет, а Роберт выходит на свободу.

Каждый заключенный — игрок, и выгода каждого может быть представлена в виде «формулы» (что получат они оба, что получит другой). Например, если я ударю тебя, моя выигрышная схема будет выглядеть так (я получаю грубую победу, ты страдаешь от сильной боли). Поскольку у каждого заключенного есть два варианта, мы можем представить результаты в таблице.

Практическое применение: Выявление социопатов

Здесь мы видим основное применение теории игр: выявление социопатов, думающих лишь о себе. Настоящая теория игр — это мощный аналитический инструмент, а дилетантство часто служит красным флагом, с головой выдающим человека, лишенного понятия чести. Люди, делающие расчеты интуитивно, считают, что лучше поступить некрасиво, потому что это приведет к более короткому тюремному сроку независимо от того, как поступит другой игрок. Технически это правильно, но только если вы недальновидный человек, ставящий цифры выше человеческих жизней. Именно поэтому теория игра так популярна в сфере финансов.

Настоящая проблема дилеммы заключенного в том, что она игнорирует данные. Например, в ней не рассматривается возможность вашей встречи с друзьями, родственниками, или даже кредиторами человека, которого вы посадили в тюрьму на 10 лет.

Хуже всего то, что все участники дилеммы заключенного действуют так, как будто никогда не слышали ней.

А лучший ход — хранить молчание, и через два года вместе с хорошим другом пользоваться общими деньгами.