112 тестов по логике с ответами

Суждение

Суждение (или высказывание) – это форма мышления, в которой что-либо утверждается или отрицается. Например:

• Если человек читает, значит, он знает буквы.
• Любой ребенок нуждается в матери.
• Все собаки – это не кошки.
• Многие цветы приятно пахнут.

Давайте рассмотрим основные свойства суждения, чтобы понять, чем оно отличается от понятия.

1. Любое суждение состоит из связанных между собой понятий. Для примера возьмем два понятия – мужчина и женщина. Из них можно составить несколько суждений:

• мужчины и женщины – это люди;
• мужчины не являются женщинами;
• некоторые женщины сильнее мужчин.

1. Любое суждение выражается в форме предложения (в то время как понятие выражается словом). При этом не каждое предложение обязательно должно быть суждением.
2. Любое суждение является либо истинным, либо ложным. Если оно соответствует действительности, оно истинное, а если не соответствует – ложное.
3. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединенных каким-либо союзом.

Из всего вышесказанного вытекает, что суждение представляет собой гораздо более сложную форму логического мышления, чем понятие. Именно поэтому в суждении выделяют четыре части: субъект, предикат, связку и квантор.

Не пугайтесь этих слов, они вовсе не так сложны, как кажется на первый взгляд. Кратко рассмотрим их.

Субъект (S) – это то, о чем идет речь в суждении. В суждении «Все растения не животные» речь идет о растениях, поэтому в данном случае субъектом являются растения.

Предикат (Р) – это то, что говорится о субъекте. В том же суждении «Все растения не животные» о субъекте «растения» говорится, что они – «не животные», поэтому предикатом данного суждения выступает понятие «животные».

Связка – это то, что соединяет субъект и предикат. Роль связки могут выполнять самые разные слова: есть, является, находится, это и т. п.

Квантор – это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, каждый пятый, половина, ни один и т. п.

Для закрепления давайте проанализируем простое суждение «Многие школьники любят физкультуру».

1. Субъект – «школьники»
2. Предикат – «физкультура»
3. Связка – «любят»
4. Квантор – «многие»

Надеемся, что это понятно. Стоит также отметить, что в некоторых суждениях квантор может отсутствовать. Однако он обязательно подразумевается. В суждении «Бабочки – это насекомые» квантор видимым образом отсутствует, но он подразумевается – это слово «все».

Вопросы в логике

Теперь давайте разберемся с тем, что такое вопрос, и почему его правильность так важна для логики.

Дело в том, что сам по себе вопрос очень близок к суждению. По сути, вопрос – это логическая форма, направленная на получение ответа в виде суждения.

Любой вопрос состоит из двух частей:

1. Основной (базисной), выраженной неким суждением (предпосылка вопроса);
2. Искомой, указывающей на необходимость дополнения этого суждения каким-то ответом.

С точки зрения логики одним из основных требований к постановке вопроса является истинность суждения базисной части. В противном случае вопрос считается логически некорректным.

Например, вопрос: «В каком году Достоевский написал «Войну и мир»?» следует признать логически некорректным, так как его базисная часть выражена ложным суждением «Достоевский написал «Войну и мир»».

Когнитивные искажения

Как показывают исследования так называемого обыденного мышления, люди «с улицы», не изощренные в академической логике, подозрительно похожи на «чужаков» Фреге. И получается, что все мы, даже логики, которые тоже живут иногда обыденной жизнью, — странные безумцы, допускающие массу отклонений от логических канонов, причем не только от классической логики, но и от всех более или менее известных логических систем.

Люди в обыденных рассуждениях допускают когнитивные искажения, демонстрируют то, что называется предвзятостью мнения: держатся до последнего за приобретенные мнения, не отказываются от них даже под давлением очевидных аргументов. Мы, особенно будучи детьми, страдаем когнитивным эгоцентризмом, то есть склонны рассматривать себя как центр мира и, соответственно, применяем разные критерии для оценки своих мнений и мнений других людей, не способны занять позицию другого человека (или, по крайней мере, делаем это с трудом). Особенные логические затруднения вызывают рассуждения с кондиционалами — то есть с условными высказываниями типа «если…, то…».

Формальная логика (ред. Чупахин И.Я., Бродский И.Н.)

Название:  Формальная логика

Под редакцией: Чупахин И.Я., Бродский И.Н.

Ленинград: Издательство Ленинградского университета, 1977.- 357 с.DjVu 3,77 Мб

Качество: сканированные страницы, текстовый слой

Язык: Русский

В основу учебника положен курс логики, читавшийся на философском факультете Ленинградского университета в течение ряда лет. В нем освещаются вопросы, относящиеся к общей и символической логике. Учебник предназначен для студентов-философов и студентов других гуманитарных факультетов и педагогических вузов.

Введение 3 § 1. Марксистская философия о мышлении — § 2. Мышление и язык 4 § 3. Определение формальной логики 5 § 4. Логика и психология 9 § 5. Из истории логики 10 § 6. Практическое значение формальной логики 16 § 7. Структура формальной логики 19

Часть первая. ОБЩАЯ ЛОГИКА. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФОРМЫ И МЕТОДЫ МЫШЛЕНИЯ

Глава I. Понятие§ 8. Об определении и структуре понятия§ 9. Основные методы образования понятий§ 10. Соотношение между содержанием и объемом понятия§ 11. Виды понятий§ 12. Формально-логические отношения между понятиями по содержанию и по объему § 13. Обобщение и ограничение понятийГлава II. Суждение§ 14. Сущность суждения и его строение§ 15. Суждение и предложение § 16. Суждение и вопрос § 17. Деление суждений по качеству и количеству§ 18. Объединенная классификация суждений по качеству и количеству§ 19. Распределеиность терминов в категорических суждениях§ 20. Отношения между суждениями§ 21. Деление суждений по модальности§ 22. Сложные сужденияГлава III. Основные формально-логические законы§ 23. Обшие замечания § 24. Закон тождества§ 25. Закон противоречия§ 26. Закон исключенного третьего§ 27. Закон достаточного основания Глава IV. Умозаключение § 28. Определение умозаключения§ 29. Непосредственные умозаключения § 30. Простой категорический силлогизм § 31. Сокращенные, сложные и сложносокращенные категорические силлогизмы§ 32. Условные, разделительные и условно-разделительные силлогизмы§ 33. Индуктивные умозаключения § 34. АналогияГлава V. Логические методы научного мышления§ 35. Методы классификации объектов исследования§ 36. Определение§ 37. Доказательство§ 38. Доказательство (продолжение: паралогизмы, софизмы и парадоксы)§ 39. Аксиоматический метод§ 40. Индуктивные методы установления причинной связи явлений § 41. Гипотеза§ 42. Вероятностные методы в логикеЧасть вторая. СИМВОЛИЧЕСКАЯ ЛОГИКАГлава I. Табличное построение логики высказываний§ 1. Высказывания и формы высказываний§ 2. Язык логики высказываний§ 3. Семантика логических знаков§ 4. Таблицы формул логики высказываний§ 5. Равносильные формулы § 6. Правило равносильной замены § 7. Полные системы логических знаков§ 8. Закон двойственности§ 9. Тождественно-истинные и тождественно-ложные формулы Глава II. Нормальные формы формул логики высказываний§ 10. Нормальная форма§ 11. Проблема разрешения§ 12. Конъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма§ 13. Логическое следование и логические следствия§ 14. Сокращенная конъюнктивная нормальная форма§ 15. Дизъюнктивные нормальные формыГлава III. Естественный вывод в логике высказываний§ 16. Понятия логического вывода§ 17. Производные правила§ 18. Чисто прямое доказательство§ 19. Слабое косвенное доказательство§ 20. Квазисильное косвенное доказательство§ 21. Сильное (классическое) косвенное доказательство§ 22. Полнота классического нечисления высказываний§ 23. Аксиоматическое представление логики высказыванийГлава IV. Формализованная силлогистикаГлава V. Естественный вывод в логике предикатовГлава VI. Модальная логика

• Назад

• Вперёд

Формы логического мышления

Форма мышления – это структура мысли, определяющая взаимосвязи между отдельными её элементами.

Существует три основных формы мышления:

1. Понятие. Это мысль о конкретном объекте, явлении или свойстве. Это может быть кто-то одушевленный (другой человек), что-то материальное (автомобиль) или нематериальное (любовь).
2. Суждение. Это цепочка взаимосвязанных понятий. К примеру, у нас есть понятие о том, что ответственность – это хорошо. И если мы думаем о том, что какой-то человек ответственный – это суждение, состоящее из двух понятий (человек + качество).
3. Умозаключение. Это вывод, который делается на основе нескольких суждений и при этом содержит в себе новую информацию. К примеру, если мы знаем, что наш знакомый является ответственным человеком, мы можем сделать вывод, что ему можно доверять.

Какие бы мысли ни крутились сейчас в вашей головы, каждая из них относится к одной из этих трёх форм. Наш жизненный опыт включает знание миллионов разных понятий, которые мы мгновенно объединяем в суждения и делаем на их основе определённые умозаключения.

Формальная логика

Относительная самостоятельность логической формы, ее независимость от конкретного содержания мысли открывает благоприятную возможность для отвлечения от этого содержания, вычленения логической формы и ее специального анализа. Этим и определяется существование логики как науки. Этим же объясняется и наименование — «формальная логика».

Но это вовсе не означает, будто она проникнута духом формализма, оторвана от реальных процессов мышления и преувеличивает значение формы в ущерб содержанию. С этой точки зрения логика сходна с другими науками, исследующими формы чего-либо:

• геометрией как наукой о пространственных формах и их отношениях,
• морфологией растений и животных,
• юридическими науками, исследующими формы государства и права.

Логика — такая же глубоко содержательная наука. А активность логической формы по отношению к содержанию делает необходимым ее специальный логический анализ, раскрывает значение логики как науки.

Все изучаемые логикой формы мышления (понятие, суждение, умозаключение, доказательство, теория) имеют прежде всего то общее, что они

1. лишены наглядности и
2. неразрывно связаны с языком.

В то же время они качественно отличны друг от друга как по своим функциям, так и по структуре. Главное отличие их как структур мысли состоит в степени их сложности. Это разные структурные уровни мышления:

• • Понятие, будучи относительно самостоятельной формой мысли, входит составной частью в суждение.
  • Суждение, в свою очередь, будучи относительно самостоятельной формой, в то же время выступает составной частью умозаключения.
  • Умозаключение — составная часть доказательства, которое само входит звеном в теорию.

Таким образом, они представляют собой не рядом стоящие формы, а иерархию этих форм. И в этом отношении они подобны структурным уровням самой материи — элементарным частицам, атомам, молекулам, телам.

Сказанное вовсе не означает, что в реальном процессе мышления сначала образуются понятия, затем эти понятия, соединяясь, дают начало суждениям, а суждения, сочетаясь тем или иным способом, порождают затем умозаключения. Сами понятия, будучи относительно наиболее простыми, формируются как результат сложной и длительной абстрагирующей работы мышления, в которой участвуют и суждения, и умозаключения, и доказательства. Суждения, в свою очередь, складываются из понятий. Точно так же суждения входят в умозаключения, а результатом умозаключений выступают новые суждения. В этом проявляется глубокая диалектика процесса познания.

Почему логика — квадратная

Логика называется формальной потому, что работает с формой, а не содержанием, то есть с тем, как устроены предложения и как они между собой связаны. Это полезно тем, что мы можем отстраниться от смысла предложений, которые могут задевать наши чувства, и сделать правильное умозаключение без эмоционального влияния.

Давайте начнем с простых умозаключений, которые принято называть «умозаключениями по логическому квадрату».

Логика (на нашем начальном уровне) имеет дело с утвердительным предложениями — простыми суждениями, которые по двум признакам делятся на четыре группы.

2-й признак: качество

По качеству бывают утвердительные и отрицательные суждения.

Если мы объединим эти два признака, то получим четыре типа суждений, а в скобках укажем их классические обозначения:

Запомнить символьное обозначение классов суждений легко, если знать их происхождение от латинских слов “affirno” — утверждать и “nego” — отрицать, из которых были взяты гласные: первые — для общих суждений, вторые — для частных.

Вы уже догадались, что углы квадрата — четыре типа суждений. Часто его рисуют вот так:

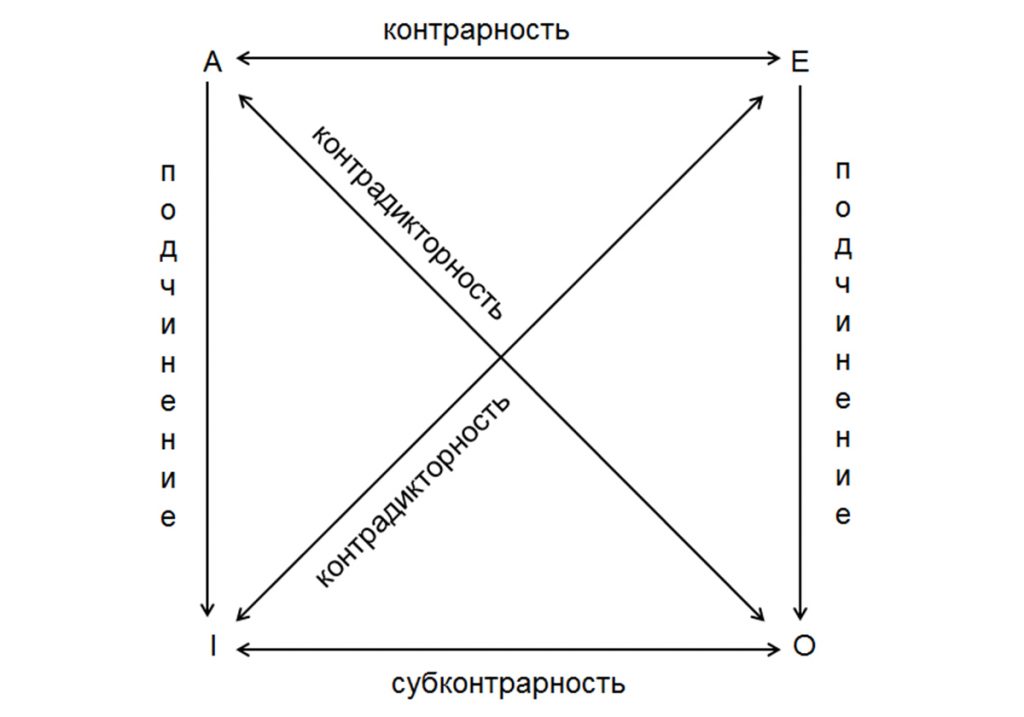
Зачем нам нужен этот квадрат? Очень просто: он показывает, в каких отношениях находятся суждения разных классов. То есть с его помощью мы можем проверять себя, правильно ли мы делаем преобразования суждений, и выяснять, куда именно закралась ошибка.

Если, если, если

Другая серия экспериментов — ее проводила Рут Берн в 1980-е годы — задачи на подавление (Suppression Task). Если мы сделали вывод modus ponens, то в классической логике никакая новая информация его не должна отменить. Рассмотрим, однако, следующие высказывания:

1. Если ей надо написать эссе, она будет допоздна работать в библиотеке. Ей надо написать эссе.

2. Если библиотека будет открыта, она будет допоздна работать в библиотеке.

3. Если у нее будет учебник, она будет допоздна работать в библиотеке.

— Она будет допоздна работать в библиотеке?

Элементарный вывод заключения (4) из посылки (1) делают 90% испытуемых. Потом добавляется вторая посылка, и тут уже только 60% делают корректный вывод, хотя мы просто добавили информацию. В случае добавления третьей посылки вновь 90% опрошенных делают правильный вывод.

Ситуация еще усложняется, когда мы вводим временной фактор:

1. Во время студенческого протеста полицейский сказал студенту: «Если войдешь в здание ректората, я тебя арестую».

2. Во время 15-минутного протеста полицейский сказал студенту: «Если войдешь в здание ректората, я тебя арестую».

3. Во время двухнедельного студенческого протеста полицейский сказал студенту: «Если войдешь в здание ректората, я тебя арестую».

4. Студент вошел в здание ректората.

— Студент будет арестован?

Больше всего корректных ответов, когда в посылке (1) вообще нет указания на время. Гораздо хуже, когда упоминается длительный период, хотя с формальной точки зрения полицейский должен арестовать студента в любом случае, вне зависимости от того, сколько времени длился протест.

Другой известный пример того, как трудно работать с кондиционалами, — мем про программиста, которому жена сказала: «Дорогой, сходи купи пакет молока, и если будут яйца, купи шесть», — и тот принес шесть пакетов молока, потому что яйца были.

Закон непротиворечия

Логическое мышление характеризуется непротиворечивостью. Противоречия разрушают мысль, затрудняют процесс познания. Требование непротиворечивости мышления выражает формально-логический закон непротиворечия.

Закон непротиворечия:

два несовместимых друг с другом суждения не могут быть одновременно истинными; по крайней мере одно из них необходимо ложно.

Закон формулируется следующим образом:

неверно, что А и не-А (не могут быть истинными две мысли, одна из которых отрицает другую).

Два противоположных суждения не могут быть одновременно ис­тинными, по крайней мере, одно из них необходимо ложь. Другими словами, при истинности одного из противоположных суждений второе необходимо ложно, но они могут быть одновременно ложными.

Т.е. нельзя одновременно утверждать и отрицать что-либо. Закон непротиворечия действует в отношении всех несовместимых суждений.

Закон непротиворечия выражается формулой ():

• • В классической логике: не может быть одновременно А и не-А, А и В.
  • В символической логике: ┐(р Λ ┐р) (неверно, что р и не-р одновременно истинны),

где р — любое высказывание, ┐р – отрицание высказывания р, знак ┐ перед всей формулой – отрицание двух высказываний, соединенных знаком конъюнкции.

Замечание

Некоторые авторы формулируют этот закон как закон противоречия:

• «А не может в одно и то же время быть В и не-В», или:
• «из двух суждений, из которых одно утверждает то, что другое отрицает, одно должно быть ложным».

Смысл этого закона заключается в том, что ничто не может в одно и тоже время, в одном и том же отношении иметь противоречащие качества.

Мы, например, никак не можем себе представить, чтобы бумага была в одно и то же время и белая и не-белая, например красная. Ни одно качество не может в одно и то же время и присутствовать и отсутствовать.

Таким образом, закон противоречия требует, чтобы мы одной и той же вещи, в одно и то же время, в одном и том же отно­шении не приписывали противоречащих предикатов В и не-В.

Подробнее о законе непротиворечия

Для правильного его понимания необходимо иметь в виду следующее:

утверждая что-либо о каком-либо предмете, нельзя, не противореча себе, отрицать (1) то же самое (2) о том же самом предмете, (3) взятом в то же самое время и (4) в том же самом отношении.

Закон противоречия выражает одно из коренных свойств логического мышления — непротиворечивость, последовательность мышления. Его сознательное использование помогает обнаруживать и устранять противоречия в своих и чужих рассуждениях, вырабатывает критическое отношение ко всякого рода неточности, непоследовательности в мыслях и действиях.

Закон непротиворечия требует от мышления непротиворечивости, после­довательности рассуждения.

Ошибка при нарушении закона непротиворечия:

«Противоречивость в рассуждении». В случае ошибки допускается следствие: (p Λ ­ р) → q, читается: если р и не-р, то q, что означает: «из лжи следует все что угодно».

Значение закона непротиворечия для работы юриста

Умение вскрывать и устранять логические противоречия, нередко встречающиеся в показаниях свидетелей, обвиняемого, потерпевшего, играет важную роль в судебной и следственной практике.

Одно из основных требований, предъевляемых к версии в судебном исследовании, состоит в том, чтобы при анализе совокупности фактических данных, на основе которых она построена, эти данные не противоречили друг другу и выдвинутой версии в целом

Наличие таких противоречий должно привлечь самое серьезное внимание следователя. Однако бывают случаи, когда следователь, выдвинув версию, которую он считает правдоподобной, не принимает во внимание факты, противоречащие этой версии, игнорирует их, продолжает развивать свою версию вопреки противоречащим фактам

Литература

• Кондаков Н. И. Логический словарь / Горский Д. П.. — М.: Наука, 1971. — 656 с.
• Arnold vander Nat. Simple formal logic: with common-sense symbolic techniques. — Routledge, 2010. — 360 с. — ISBN 978-0415997454.
• Чупахин И. Я., Бродский И. Н. Формальная логика. — Л.: ЛГУ, 1977. — 357 с.

История логики

• Маковельский А. О. История логики. — М., .
• Попов П. С. История логики нового времени. — М., .
• Logic, history of: Precursors of modern logic // Encyclopedia of philosophy / Donald M. Borchert, editor in chief. — 2nd ed. — N. Y.: Thomson Gale, 2006. — Т. 5. — С. 440—446. — 742 с. — ISBN 0-02-865785-3.
• Logic, history of: Modern logic // Encyclopedia of philosophy / Donald M. Borchert, editor in chief. — 2nd ed. — N. Y.: Thomson Gale, 2006. — Т. 5. — С. 447—484. — 742 с. — ISBN 0-02-865785-3.

Судьба формальной логики в СССР

• Алексеев М. Н. Обсуждение вопросов логики в Московском государственном университете // Вопросы философии, , № 2;
• Алексеев М. Н. Дискуссия по вопросу соотношения формальной логики и диалектики // Вестник МГУ, Серия I. Общественные науки, 1951, № 4.
• Щедровицкий Г. П. Я всегда был идеалистом…. — М., 2001. — 323 с. — ISBN 5-93733-010-2.

Закон тождества

Любая мысль в процессе рассуждения должна иметь определенное, устойчивое содержание. Это коренное свойство мышления — его определенность — выражает закон тождества.

Закон тождества:

всякая мысль в процессе познания должна быть тождественна самой себе (а есть а, где под а понимается любая мысль).

Или, всякая мысль в процессе рассуждения должна быть тождественна самой себе:

1. 1. Об одном и том же;
   2. То же самое;
   3. В одно и то же время;
   4. В одном и том же отношении.

Другими словами, объем и содержание мыслей должны быть уточнены и оставаться неизменными до конца рассуждения.

Закон тождества может быть выражен формулой:

• • В классической логике: А есть А; А = А, где под А понимается любая мысль.
  • В символической логике: р → р (если р, то р), где р – любое высказывание, → — знак импликации.

Следствия из закона тождества:

1. 1. нельзя отождествлять различные мысли;
   2. нельзя тождественные мысли принимать за нетождественные.

Закон тождества требует от мышления точности, ясности, определенно­сти, адекватности, однозначности.

Ошибка при нарушении закона тождества:

Отождествление различных понятий представляет собой логическую ошибку – подмену понятия, которая  может быть как неосознанной, так и преднамеренной.

Пример

Например, одно ли и тоже сначала сказать: «У него болит голова», затем – «У него что-то с головой», а потом – «Больной на всю голову»? Естественно, что в данном примере произошла преднамеренная подмена первоначальной мысли.

Причины нарушения закона тождества:

1. 1. логическая – отсутствие логической культуры, нетребовательность к точности мысли;
   2. лингвистическая – омонимичность языка (наличие в нем разных позначению, но одинаковых по звучанию и написанию слов);
   3. психологическая – ассоциативность мышления.

Нарушение этих требований в процессе рассуждения нередко бывает связано с различным выражением одной и той же мысли в языке.

Употребление многозначных слов может привести к ошибочному отождествлению различных мыслей.

Значение закона тождества для работы юриста

Соблюдение требований закона тождества имеет важное  значение в работе юриста, требующей употребления понятий в их точном значении. При разбирательстве любого дела важно выяснить точный смысл понятий, которыми пользуется обвиняемый или свидетели, и употреблять эти понятия в строго определенном смысле. В противном случае предмет мысли будет упущен и вместо выяснения дела произойдет его запутывание

В противном случае предмет мысли будет упущен и вместо выяснения дела произойдет его запутывание.

Закон достаточного основания

Четвертый из основных законов формальной или классической логики был сформулирован по прошествии значительного периода времени после обоснования Аристотелем первых трех. Его автор – видный немецкий ученый (философ, логик, математик, историк; этот список занятий можно продолжить) – Готфрид Вильгельм Лейбниц. В своей работе о простых субстанциях («Монадология», 1714 г.) он писал: «…ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым, – без достаточного основания, почему именно дело обстоит так, а не иначе, хотя эти основания в большинстве случаев вовсе не могут быть нам известны».

Современное определение закона Лейбница основано на понимании, что всякое положение для того, чтобы считаться вполне достоверным, должно быть доказанным; должны быть известны достаточные основания, в силу которых оно считается истинным.

Функциональное предназначение данного закона выражается в требовании соблюдать в мышлении такую черту, как обоснованность. Г. В. Лейбниц, по сути, объединил законы Аристотеля с их условиями определенности, последовательности и непротиворечивости рассуждения, и на основании этого разработал понятие о достаточном основании для того, чтоб характер размышления был логичным. Немецкий логик хотел этим законом показать, что в познавательной или практической деятельности человека рано или поздно наступает момент, когда недостаточно иметь просто истинное утверждение, нужно чтобы оно было обоснованным.

При детальном анализе оказывается, что закон достаточного основания мы применяем в повседневной жизни довольно часто. Делать выводы, основываясь на фактах – значит применять этот закон. Школьник, указывающий в конце реферата список использованной литературы и студент, оформляющий ссылки на источники в курсовой работе – этим они подкрепляют свои выводы и положения, следовательно, используют закон достаточного основания. С тем же самым люди разных профессий сталкиваются в процессе своей работы: доцент – при поиске материала для научной статьи, спичрайтер – при написании речи, прокурор – во время подготовки обвинительного выступления.

Нарушение закона достаточного основания также широко распространено. Иногда причиной тому неграмотность, иногда – специальные уловки с целью получения выгоды (например, построение аргументации с нарушением закона для победы в споре). Как пример, высказывания: «Этот человек не болеет, у него ведь нет кашля» или «Гражданин Иванов не мог совершить преступление, ведь он прекрасный работник, заботливый отец и хороший семьянин». В обоих случаях ясно, что приводимые аргументы в недостаточной мере обосновывают тезис, а, значит, являются прямым нарушением одного из основных законов логики – закона достаточного основания.

Интересуетесь развитием логического мышления и мышления глобально? Обратите внимание на курс «Когнитивистика»»

Никто или некоторые?

Вот, например, исходное общеотрицательное суждение, которое можно сделать из отрицания знаменитого мифа о том, что люди используют свой мозг только на 10 %.

Оно дает нам на самом деле довольно мало информации. Мы можем вывести из него «некоторые не используют мозг на 10 %». По-русски эту звучит весьма неоднозначно — и это еще одна проблема использования естественного языка в формальной логике, но об этом в другой раз.

Возьмем за изначальное суждение частноотрицательное:

Какой вывод из этого можно сделать? Некоторые делают вывод, что врачи травят людей таблетками и нужно лечиться чем-то «натуральным». На самом деле можно сделать лишь один вывод: общеутвердительное суждение «все таблетки лечат» не является истинным — что никогда не вызывало сомнений, особенно учитывая, что медикаменты довольно часто употребляют без рекомендации врачей.

Для закрепления расшифруем связи в квадрате, которые еще не называли, и перейдем к рассмотрению некоторых типичных ошибок, связанных с умозаключениями по логическому квадрату:

Утрата специфики

Распространение идей многозначной логики в различных её вариантах (в том числе, символизированных), а затем — идей абстрактных типов данных в теоретическом программировании проблематизировало «изнутри» специфику истинности как области значений логических функций, включающих лишь два возможных значения. Так, аппарат бесконечнозначной логики Лукасевича—Тарского практически неотличим от аппарата теории вероятностей, а в теории типов данных логический (булев) тип ничем особенным не отличается от прочих ни с операторной точки зрения, ни с точки зрения машинной реализации.

С другой стороны, новые разделы и версии символической логики (например, интуиционистская логика, интенциональная логика, деонтическая логика) вышли далеко за пределы силлогистики и исследования истинности в узком смысле и охватили собой многие другие разделы логики.

В настоящее время термин «формальная логика» утратил специфическое значение и применяется (вне контекста истории науки) как синоним символической, или математической логики. «Традиционной» (в противоположность «современной») формальной логикой могут называть те же разделы логики, изложенные без применения математического аппарата.

Закон тождества

Первый и наиболее важный закон логики – это закон тождества, который был сформулирован еще Аристотелем.

Закон тождества утверждает, что любая мысль (любое рассуждение) обязательно должна быть равна (тождественна) самой себе, т. е. она должна быть ясной и точной, простой и определенной.

Говоря иначе, этот закон запрещает путать и подменять понятия в рассуждении (т. е. употреблять одно и то же слово в разных значениях или вкладывать одно и то же значение в разные слова), создавать двусмысленность и т. п.

Например, смысл простого на первый взгляд высказывания «Студенты прослушали лекцию преподавателя» непонятен, потому что в нем нарушен закон тождества. Ведь слово «прослушали» можно истолковать двояко: то ли студенты внимательно слушали преподавателя, то ли все пропустили мимо ушей.

Получается, что высказывание было одно, а возможных значений у него два, вследствие чего нарушается тождество: 1 ≠ 2. Другими словами, в приведенном высказывании смешиваются (отождествляются) две различные (нетождественные) ситуации.

Если закон тождества нарушается непроизвольно (по незнанию или по невнимательности), тогда возникают просто логические ошибки. Если же это делается преднамеренно, с целью запутать собеседника и доказать ему какую-нибудь ложную мысль, то это уже не просто ошибки, а софизмы, о которых мы писали выше.

Интересен факт, что многие смешные афоризмы, анекдоты, задачи и головоломки построены именно на нарушении логического закона тождества. Например:

***

Не стой где попало, а то еще попадет.

***
– Я сломал руку в двух местах.

– Больше не ходи в эти места.

***

– Зачем (за чем) вода в стакане?

– Чтобы ее пить.

– Нет, за стеклом!

***

Все или некоторые? Делаем правильные выводы

Обычно мы делаем логические преобразования со сложными для анализа суждениями. Но мы рассмотрим силу логического квадрата на примере содержательно простых суждений.

Предположим, что мы думаем так:

Какие выводы мы можем из этого сделать? Это общеутвердительное (А) суждение, следовательно, мы можем сказать, что:

— это тоже верное суждение, так как оно частноутвердительное (I) и (смотрим на квадрат) находится в отношении подчинения с A. Все отрицательные суждения при этом будут ложными, неправильными, так как они будут контрарными (общеотрицательные E) и контрадикторными (частноотрицательные O) по отношению к изначальному суждению (общеутвердительные A). То есть неправильно будет сказать «некоторые мужики — не козлы».

Несколько интереснее получается, если у нас исходное суждение частноутвердительное:

Можно ли из этого сделать вывод, что все бабы дуры? Нет, из частного нельзя вывести общее, только наоборот: отношение подчинения в квадрате — одностороннее! Вот так-то.

А что с отрицательными суждениями?

Умозаключение

Умозаключение – это форма мышления, в которой из двух или нескольких суждений, называемых посылками, вытекает новое суждение, называемое заключением (выводом). Например:

• Все животные нуждаются в корме.
• Лошади – это животные.
• Лошади нуждаются в корме.

В приведенном примере первые два суждения являются посылками, а третье – выводом (умозаключением).

Имейте в виду, что посылки должны быть не только истинными суждениями, но и связанными между собой.

Умозаключения делятся на три вида:дедуктивные, индуктивные и умозаключения по аналогии.

Дедуктивные умозаключения (дедукция) (от лат. deductio — «выведение») – это умозаключения, в которых из общего правила делается вывод для частного случая. Например:

• Все хищники питаются мясом.
• Львы – это хищники.
• Львы питаются мясом.

Основное достоинство дедукции заключается в достоверности ее выводов. Известный персонаж Шерлок Холмс пользовался дедуктивным методом при раскрытии преступлений.

Однажды, объясняя доктору Ватсону суть дедуктивного метода, он привел такой пример. Около убитого полковника была найдена выкуренная сигара, вследствие чего сыщики Скотленд-Ярда решили, что именно он выкурил ее перед смертью. Но Холмс отвергает эту версию на основании того, что полковник носил большие усы, а сигара выкурена до конца.

Иначе говоря, если бы ее курил убитый, то он обязательно бы подпалил свои усы. Следовательно, делает дедуктивное умозаключение Холмс, сигару выкурил другой человек.

Все дедуктивные умозаключения называются силлогизмами (от греч. sillogismos – «подсчитывание, подытоживание, выведение следствия»).

Индуктивные умозаключения (индукция) (от лат. inductio — «наведение») – это умозаключения, в которых из нескольких частных случаев выводится общее правило. Например:

• Петя любит играть.
• Ваня любит играть.
• Настя любит играть.
• Петя, Ваня и Настя – дети.
• Все дети любят играть.

Умозаключения по аналогии (аналогия) (от греч. analogia — «соответствие») – это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. Например:

• Мотоциклист Вася обожает свой мотоцикл, быструю езду, ровную дорогу, и недолюбливает машины.
• Мотоциклист Коля обожает свой мотоцикл, быструю езду и ровную дорогу.
• Вероятно, Коля недолюбливает машины.

Помните, что выводы аналогии и индукции всегда вероятностны.

Итак, вы ознакомились с определением науки логики, а также поняли, что собой представляет логическое мышление.

Теперь вам осталось совсем немного, а именно, узнать 4 основных закона логики. После этого вы сможете развивать логическое мышление и определять логические ошибки своих собеседников.